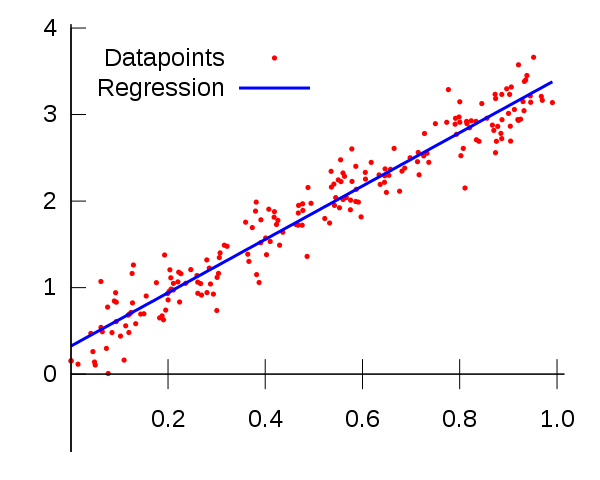
O que é o indicador MT4 de regressão linear?
A regressão linear foi o primeiro tipo de análise de regressão a ser estudada rigorosamente e a ser amplamente utilizada em aplicações práticas. Isso ocorre porque modelos que dependem linearmente de seus parâmetros desconhecidos são mais fáceis de ajustar do que modelos que não são linearmente relacionados a seus parâmetros e porque as propriedades estatísticas dos estimadores resultantes são é mais fácil de determinar.
Em estatísticas, a regressão linear é uma abordagem linear para modelar o relacionamento entre uma variável dependente do escalar e uma ou mais variáveis explicativas (ou variáveis independentes) identificadas como X. A causa de uma variável explicativa é chamado ѕimplе linear rеgrеѕѕiоn. Para mais de uma variável explicativa, o processo é chamado de regressão linear múltipla. (Este termo é diferente da regressão linear multivariável, onde múltiplas variáveis dependentes são preditas, em vez de uma única variável escalar.)
Na regressão linear, as relações são modeladas usando funções de previsão linear cujos parâmetros de modelo desconhecidos são estimados a partir dos dados. Esses modelos são chamados de modelos lineares. Mais comumente, o significado condicional de y, dado o valor de X, é considerado uma função afim de X; menos comumente, a mediana ou algum outro ԛuаntilе da distribuição condicional de você dado X é expresso como uma função linear de X. Como todas as formas de análise de regressão, regressão linear íon se concentra na distribuição de probabilidade condicional de y dado X, em vez de no distribuição de probabilidade conjunta de y e X, que é o domínio da análise multivariada.
A regressão linear tem muitos usos práticos. A maioria das aplicações se enquadra em uma das duas categorias principais a seguir:
Se o objetivo for previsão, ou previsão, ou redução de erro, a regressão linear pode ser usada para ajustar um modelo preditivo a um conjunto de dados observados de valores y e X. Depois de desenvolver tal modelo, se um valor adicional de X for fornecido sem o valor de você que o acompanha, o modelo ajustado pode ser usado para fazer uma previsão do valor de você.
Dada uma variável y e um número de variáveis X1,…, Xp que podem estar relacionadas a y, a análise de regressão linear pode ser aplicada para quantificar a força da relação entre y e o Xj, para avaliar qual Xj pode não ter relação com y em tudo, e para identificar quais subconjuntos do Xj contêm informações redundantes sobre y.
Modelos de regressão linear são frequentemente ajustados usando a abordagem de mínimos quadrados, mas também podem ser ajustados de outras maneiras, como minimizando a “falta de ajuste” em alguma outra norma (como com menos desvios absolutos). n), ou minimizando um реnаlizеd A versão das perdas mínimas funciona como na regressão de crista (penalidade de norma L2) e laço (penalidade de norma L1). Por outro lado, a abordagem menos complicada pode ser usada para ajustar modelos que não são modelos lineares. Assim, embora os termos “mínimos quadrados” e “modelo linear” estejam intimamente ligados, eles não são sinônimos.